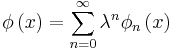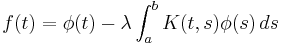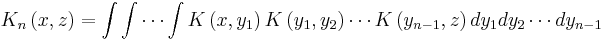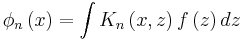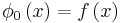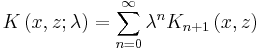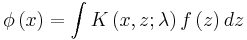Liouville–Neumann series

In mathematics, the Liouville–Neumann series is an infinite series that corresponds to the resolvent formalism technique of solving the Fredholm integral equations in Fredholm theory.

Definition

The Liouville–Neumann series is defined as

$\phi\left(x\right) = \sum^\infty_{n=0} \lambda^n \phi_n \left(x\right)$

which is a unique, continuous solution of a Fredholm integral equation of the second kind:

$f(t)= \phi(t) - \lambda \int_a^bK(t,s)\phi(s)\,ds$

If the nth iterated kernel is defined as

$K_n\left(x,z\right) = \int\int\cdots\int K\left(x,y_1\right)K\left(y_1,y_2\right) \cdots K\left(y_{n-1}, z\right) dy_1 dy_2 \cdots dy_{n-1}$

then

$\phi_n\left(x\right) = \int K_n\left(x,z\right)f\left(z\right)dz$

with

$\phi_0\left(x\right) = f\left(x\right)$

The resolvent or solving kernel is given by

$K\left(x, z;\lambda\right) = \sum^\infty_{n=0} \lambda^n K_{n%2B1} \left(x, z\right)$

The solution of the integral equation becomes

$\phi\left(x\right) = \int K \left( x, z;\lambda\right) f\left(z\right)dz$

Similar methods may be used to solve the Volterra equations.